
mean density of common substances (useful in calculating the mass/weight and the moments of inertia)Ī sphere (from Greek - sphaira, "globe, ball") is a perfectly round geometrical and circular object in three-dimensional space that resembles the shape of a completely round ball.moment of inertia of a spherical shaped object based around the edge of the sphere.moment of inertia of a spherical shaped object based around the central axis (diameter).Sphere Segment Full Surface Area (with the top and bottom circles, aka ends).Sphere Segment Wall Surface Area (without the circular top and bottom ends).Sphere Weight (Mass) based on volume and mean density (mD).Note, different units are available for input and outputs of the equations. See our sphere math worksheets here in the Kami Library.The Sphere Calculator contains equations for volumes, surface areas, and moments of inertia for objects shaped like a geometric sphere. The user can enter basic dimensions and the calculator returns the values. What other ways can you think of that we can find a connection between the volume of a sphere and real-life?
#Sphere geometry calculator how to
These are just a few of the many real-life applications that are affected by knowing how to calculate the volume of a sphere. This is a critical component of physics and engineering with sound design.įor packaging and manufacturing, designers use the calculations from determining the volume of a sphere to assist in knowing the size and capacity for various containers to efficiently and attractively pack up and display spherically shaped objects such as ball bearings, sports balls, medicine capsules, etc. When designing submarines, ships, and other watercraft items, knowing how to calculate the volume of a sphere helps with determining the buoyancy of the items.
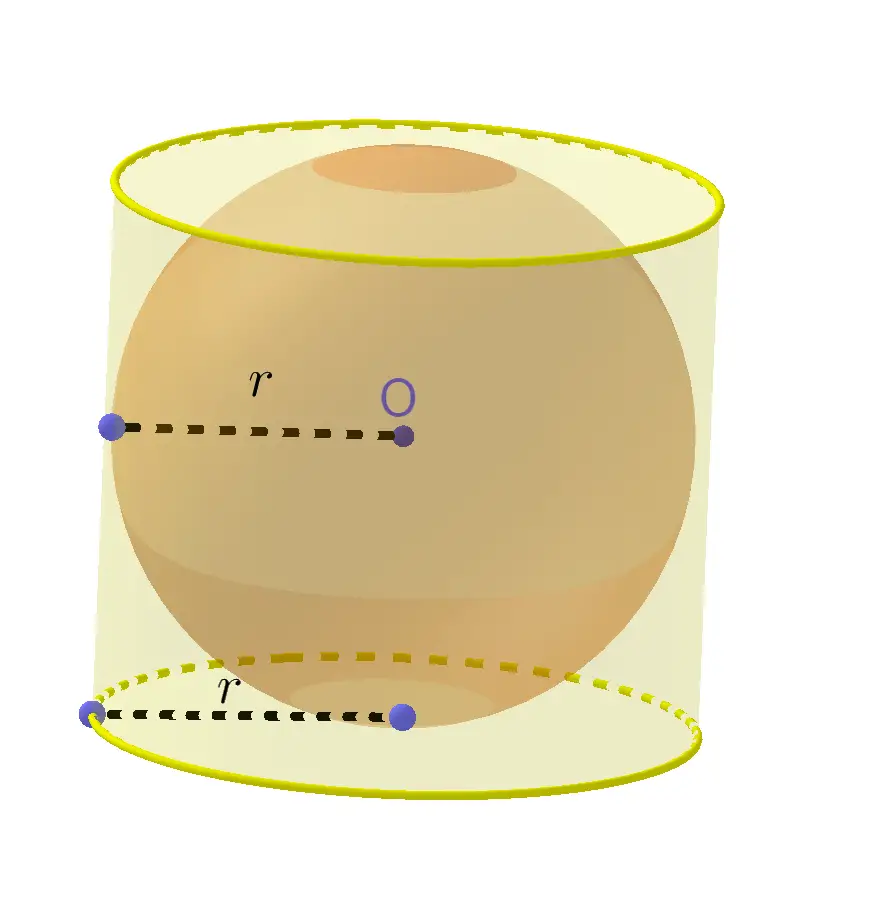
It also aids in the measurement of ingredients for food preparation. In cooking, understanding the volume of a sphere as well as a generic base of knowledge for spatial relations helps when preparing round-shaped dishes, such as cakes, cookies, meatballs, etc. Volume of a sphere has many real life applications that are spread across a wide range of areas. Knowing how to calculate the volume of a sphere is important, and not just for success inside a mathematics classroom. Here is how solving for the surface area would work with the formula:įinal answer = SA = 50.27cm 2 Real-life applications for volume of a sphere We’ll also go back to the chocolate candy example we used to find the volume, where the radius was 2cm. To find the surface area of the sphere, we will use the formula SA = 4πr 2. You can also use a sphere calculator like this one. That means you can divide the length of the diameter in half to find out the radius.įor example, let’s say we wanted to find the total volume of a spherical chocolate candy with a radius of 2cm - this is how we’d use the volume formula: Remember – the diameter of a sphere is twice the distance of the radius. Sometimes, you might be given a sphere’s diameter in a math problem. This graphic shows a great example of a sphere’s radius. To find the volume of the sphere, the equation is V = 4/3 πr (or pi r) 3, where r is the radius of the sphere. cubic centimeters and cubic meters (or cubic inches and cubic feet) Cubic units - The units used to measure volume.Pi π - A symbol that represents the perimeter of a circle divided by the diameter of a circle, which will always equal 3.14 (to two decimal places).Volume v - The amount of space a three-dimensional object can contain inside the surface area.Surface area – the outer shell of a three-dimensional object.Diameter - A straight line that crosses a circle at its radius.Radius - The line that starts at the center of a circle and stops at the edge of a circle.Examples include cubes, triangular prisms, and spheres. Objects with 3 dimensions (a three-dimensional shape) are measured by height, length, and depth.Examples include squares, triangles, and circles. Objects with 2 dimensions (a two-dimensional shape) are measured by height and length.Dimensions - A term of measurement to help define an object’s parameters.




 0 kommentar(er)
0 kommentar(er)
